En esta entrada vamos a analizar una tabla de frecuencias sencilla empleando la distribución de probablidades de Poisson, que es un miembro de la familia exponencial de distribuciones de probabilidades, lo que nos permite encajar el análisis dentro de los Modelos Lineales Generalizados como veremos a continuación.
Los datos que vamos a analizar provienen de Sobhan Moosavi, Mohammad Hossein Samavatian, Srinivasan Parthasarathy and Rajiv Ramnath "A Countrywide Traffic Accident Dataset" (2019) que en su versión más reciente incluye el registro de accidentes en EE.UU entre Febrero de 2016 y Diciembre de 2020, disponible en kaggle.com. En concreto vamos a analizar la frecuencia de accidentes en la ciudad de New York, durante los días de la semana, ocurridos en el año 2020. Para ello es necesario descargar los datos, dar el formato adecuado a las variables fecha (en concreto la denominada "Start_Time"), extraer de estas los días de la semana, y agregar las observaciones para llegar a una tabla como la siguiente:
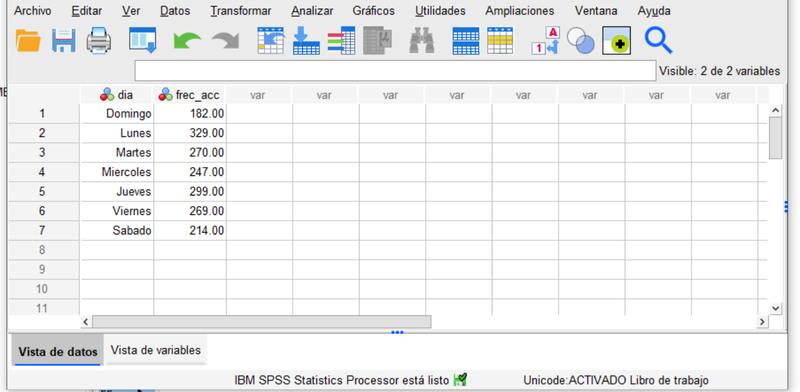
Los accidentes de tráfico son sucesos que presentan variación intrínseca, no solo cuando se consideran caso a caso, sino también cuando están agrupados en las clases que resultan de considerar el día de la semana en que acontecen.
Como veíamos en la "Pildora 2", las distribuciones de probabilidades son los modelos que empleamos para representar fenómenos esencialmente variables. Así, para modelizar la tabla de frecuencias anterior, con un único criterio de clasificación correspondiente a los 7 días de la semana , la distribución de probabilidades adecuada sería la MULTINOMIAL con 7 categorías. Ahora bien, fijado el total de observaciones (accidentes en este caso), la frecuencia de cada celda (día de la semana) se puede concebir como procedente de una distribución de POISSON con parámetro Lambda y subíndice i: 1 ,2...7 para día . [Si se quiere profundizar sobre esta relación existe abundante literatura al respecto; dejamos aquí un enlace con mayor detalle.]
Lo anterior prueba que la distribución de probabilidades de Poisson es conceptualmente adecuada para capturar la variabilidad de las frecuencias diarias de accidentes en estudio. Aceptada esta adecuación, la siguiente pregunta natural es si los siete días presentan un comportamiento variable homogéneo o, por el contrario, cabe identificar diferencias entre ellos. Para responder actuaremos incrementalmente: empezaremos por considerar el ajuste de las observaciones al modelo más simple (donde hay una distribución de probabilidades única para todos los dias) que podremos ir haciendo más complejo en función de los resultados obtenidos. En el límite, llegariamos a la conclusión de que cada día es completamente diferente de los restantes, estimando un modelo de probabilidades diferente para cada dia de la semana, con lo que nada ganariamos respecto a trabajar con la tabla anterior. En cada uno de estos pasos haremos 2 cosas: ajustar las observaciones a un modelo de variabilidad y evaluar el grado de adecuación de ese ajuste.
Lo primero que haremos será ajustar el modelo base" bajo el cual la distribución de probabilidades que genera las observaciones es la misma para todos los días de la semana. Dado que la distribución de Poisson depende de un único parámetro, Lambda, que además se identifica con la media de la distribución, es equivalente a presumir que todas las observaciones proceden de una distribución con parámetro Lambda constante.
Lo siguiente que tenemos que considerar es cómo funciona "nuestra balanza" estadística, es decir nuestro instrumento de medida que, como hemos anticipado, es el Modelo Lineal Generalizado apropiado a esta distribución de probabilidades. Bajo este modelo, la función de enlace que se iguala al predictor lineal es la logarítmica. En otras palabras, podemos trabajar con la siguiente expresión:
log(Lambda) = b0 + b1 * X1 + b2 * X2 ..
que interpretamos como: el logaritmo de la media de la distribución de probabilidades cambia según una combinación lineal de los factores y covariables cambiantes representados por X1, X2, etc.
Si como hemos anticipado, lo que vamos a ajustar y contrastar es la hipótesis de que las observaciones proceden de la misma distribución con independencia del día de la semana, entonces no hay factores ni covariables a considerar, y el modelo a ajustar se reduce a la constante: log(Lambda) = b0.
Como vemos, el modelo es lineal en la escala logarítmica, y por ello las regresiones que vamos a ajustar reciben el nombre de Logaritimico-lineales o Loglineales.
Vayamos pues al ajuste en sí. En el menú principal elegimos Analizar>Modelos lineales generalizados>Modelos lineales generalizados, y accedemos a una ventana con múltiples pestañas que nos permite detallar la especificación. En cada uno de las pestañas haremos:
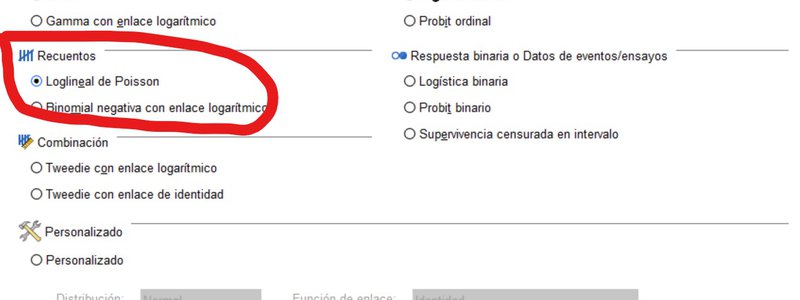
- Tipo de modelo: elegimos en la sección "Recuentos" el "Loglineal de Poisson"
- Respuesta: llevamos "Num accidentes" a la caja correspondiente a la variable respuesta
- Predictores: no realizamos ninguna selección pues estamos ajustando el modelo base sin factores ni covariables.
- Estimación: dejamos las opciones por defecto
- Estadísticas: Incluir estimación de los parámetros exponenciales
- Guardar: seleccionamos los "residuos" y "residuos de Pearson" que mide la contribución de cada celda al test Chi-cuadrado de bondad de ajuste con el signo del residuo bruto en cada caso.
Como no se va a exportar nada obviamos la última pestaña. Click en "aceptar", y tras una advertencia de que se va a ajustar un modelo de intersección (constante), los resultados (no los mostramos aquí) informan de que el ajuste presenta una desvianza de 58.5 y 6 grados de libertad (7 celdas de la tabla - 1 parámetro único). El Criterio de Información de Akaike (AIC) es de 112.22.
El modelo ajustado responde a:
log(Lambda) = 5.555
de donde se deriva que la estimación de Lambda (media de la distribución) es 258.571.
La inspección de los residuos resulta muy informativa. Recordemosque los residuos de Pearson tienden a distribuirse como una N(0,1) de modo que los valores por encima de 2 - 3 denuncien un mal ajuste de la celda (día) en cuestión:
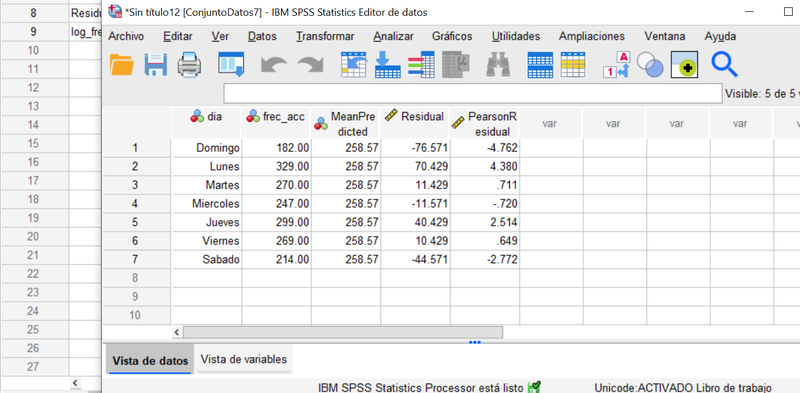
Hay claramente un efecto "fin de semana", lo que era esperable, pues el tráfico de vehículos suele ser menor durante el fin de semana; un "efecto lunes" y -posiblemente- un "efecto jueves". Como los diferentes modelos especificados alteran los resultados del ajuste, entre ellos los valores estimados y los residuos, vamos a modificar las especificaciones de los ajustes a través de modelos lineales sucesivos de complejidad incremental (incorporando cada vez mayor número de parámetros).
Proseguimos entonces con un modelo que suponga que la distribución es diferente entre el fin de semana y los restantes días. Necesitamos así añadir un factor que tome 2 valores, por ejemplo "0" para sábado y domingo, y "1" el resto de días. La función de enlace será ahora: log(Lambda) = b0 + b1 * X1 , donde X1 representa el factor mencionados cuyos valores y etiquetas habremos introducido previamente al ajuste a través de la ventana de datos.
Llamamos nuevamente al procedimiento de Modelos Lineales Generalizados del menú principal, para modificar 2 pestañas respecto a la especificación anterior:
- Predictores: trasladamos la recién creada variable "Fin de semana" al recuadro de Factores.
- Modelo: trasladamos la variable "Fin de semana" al recuadro de Modelo.
Click en "aceptar" para llegar a los resultados: la desvianza es de 16.67 con 5 grados de libertad, lo que indica un ajuste considerablemente mejor que el modelo anterior o base (donde había una media única). AIC es también mejor, 72.31 lo que indica que a pesar de ser un modelo más complejo que el anterior -pues requiere un parámetro más- las ganancias de información del ajuste empírico superan las pérdidas consecuencia de su mayor complejidad relativa.
El modelo ajustado es ahora:
log(Lambda) = 5.645 - 0.356 * X1
de forma que las medias de las distribuciones resultan 198 durante el fin de semana, y 282 el resto de días.
La inspección de los residuos resulta informativa (reparemos que también aparecen los residuos y el ajuste del primer modelo considerado que ahora ignoraremos).
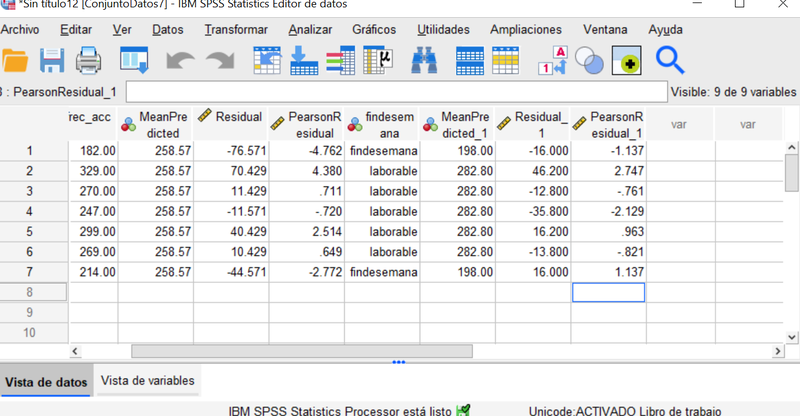
Este ajuste es considerablemente mejor, el efecto del fin de semana está perfectamente acomodado y el lunes continúa manifestándose como un día diferente. El jueves ha cedido su protagonismo al miércoles que, de todas formas, presenta un desajuste relativamente menor.
Como último paso, ajustaremos un modelo que permita cuantificar también el "efecto lunes". Necesitamos un factor con 3 niveles, 0 para el fin de semana, 1 para los lunes y 2 para los restantes días, que introducimos oportunamente a través de la ventana de datos con el nombre de "fin_sem_lunes".
Para ajustar este modelo procedemos exactamente igual que en el caso anterior, substituyendo -en las pestañas de "Predictores" y "Modelo"- el factor "findesemana" -empleado anteriormente- por el nuevo "fin_sem_lunes," dejando inalteradas las restantes especificaciones.
La desvianza de este nuevo ajuste es 7.59 con 4 grados de libertad presentando ganancias con respecto al modelo anterior que se confirman con una leve mejora del AIC que pasa a 65.23. Las nuevas medias para las tres distribuciones de Poisson correspondientes a "fin de semana," "lunes "y "resto de días" se estiman, respectivamente, en 198, 329 (igual a la frecuencia observada como no podía ser de otra forma) y 271.25 accidentes diarios.
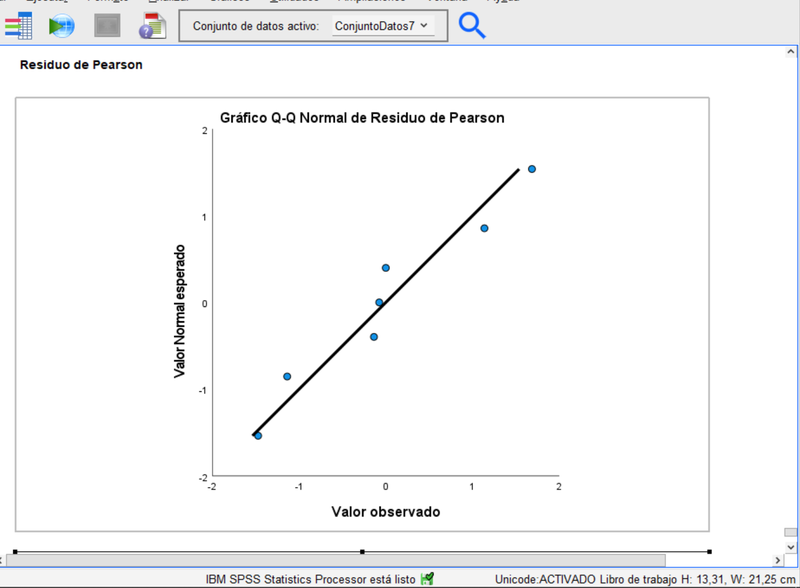
Los residuos confirman la bondad de este nuevo ajuste:
El grafico Q-Q que compara, en este caso, los cuantiles de los Residuos de Pearson estimados por el modelo ajustado y los teóricamente procedentes de una distribución normal, confirman la idoneidad de ajuste. (Analizar>Estadísticos Descriptivos>Gráficos Q-Q y trasladar los residuos de Pearson del ultimo modelo ajustado al recuadro de "Variables", aceptando al final.)
Conclusión: la distribución de frecuencias del número de accidentes por día de la semana, soporta la hipótesis de que responde a 3 procesos de Poisson diferentes. Por un lado los fines de semana, con una frecuencia media relativamente menor, en segundo lugar el que hemos denominado "efecto lunes" con una media significativamente mayor y, por último, los restantes días que presentan un comportamiento razonablemente homogéneo. En otras palabras, empleando distribuciones de probabilidad que nos permiten acomodar la variación, hemos conseguido caracterizar la distribución de frecuencias de los accidentes de tráfico a través de 3 entidades (3 distribuciones de Poisson) en vez de las 7 entidades incialmente consideradas en la tabla (una celda para cada día de la semana). Esta forma de proceder es análoga para tablas con más dimensiones (más de un criterio único de clasificación), si bien las cosas se complican un poco más como vermos oportunamente.
Para terminar: la explicación del comportamiento diferente de los accidentes entre los días de la semana requiere de un marco conceptual extra-estadístico que está fuera del alcance pretendido en este blog.